Jean-Baptiste Hiriart-Urruty

Membre de l’Académie depuis 2004
Professeur de mathématiques à l’Université Paul Sabatier de Toulouse.
Activités

14 Février 2019 : Conférence à la mairie de Pechbusque, salle du conseil « Pierre de Fermat : magistrat, philologue et mathématicien illustre mais … énigmatique »
Publication Annoncée

Publications





——————————–
Divers et curiosités
Epatez vos amis avec des mathématiques élémentaires !
Prenons une corde tendue au sol entre deux poteaux de football distants de 100 mètres, poteaux auxquels les extrémités de la corde sont attachées. On ajoute juste 1 mètre à la corde, ce qui lui donne un peu de mou… Au milieu du terrain, à 50 mètres de chaque poteau donc, on tire la corde vers le haut, le plus possible, de façon que la disposition résultante ait la forme d’un chapeau ou d’un triangle bien aplati.
Question : A quelle hauteur h est le sommet le plus haut du triangle ?
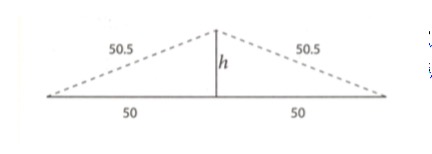
Posez la question autour de vous, et les réponses fuseront : “C’est à peine perceptible, l’allongement de la corde n’a été que de 1%…” ; “Quelques centimètres à peine, un ballon de foot ne passerait pas dessous… ” ; “Moins de 1mètre en tout cas… ” (là, je hoche la tête pour laisser penser que je vais dans son sens… ). Mais, quelle est la réponse exacte ? Eh bien, elle est surprenante : plus de 7 mètres ! Une maison passerait dessous…
Devant l’incrédulité de vos interlocuteurs, il n’y a plus qu’à faire une démonstration.. très simple au demeurant (niveau classe de Troisième) sans recours à une quelconque formule de trigonomètrie… La voici.
A l’aide de notre bon vieux théorème de Pythagore, on écrit : (50)2 + h2 = (50, 5)2 ,
h2 = (50, 5)2 − (50)2 .
Et là, on se souvient de l’identité remarquable a2 − b2 = (a + b) (a − b), de sorte que h2 =100,5×0,5=50,25.
Ainsi h = 50,25 > 7 (puisque 7 = √49).
Etonnant, non ?
+++++++++
Eh Oh, année 2019 !
– Le nombre 2019 a quelques particularités, c’est par exemple la somme de 3 carrés de nombres entiers :
2019 = (.)2 + (.)2 + (.)2, (D)
mais ce n’est pas la somme de 2 carrés d’entiers, comme c’est le cas pour ses voisins 2018 et 2020. Les mathématiciens savent dire quand cela est possible et quand ça ne l’est pas… Reste à trouver effectivement ces décompositions. On peut décomposer 2019 comme indiqué dans (D) de 9 façons différentes… On est sympa, on vous en donne (presque) une :
2019 = (31)2 + (.)2 + (.)2,
les deux nombres manquants sont égaux.
– A part ̧ca, 2019 est l’année du 50e anniversaire du premier vol du Concorde à Toulouse (mars) 50e anniversaire des premiers pas de l’homme sur la lune (juillet) 30e anniversaire de la chute du mur de Berlin (novembre).
++++++++

2009 Année « magique » : ( . est le symbole de la multiplication ci-dessous)
7.(7.7.7 – 7.7 – 7) = 2009 (soit 7 fois le chiffre 7 !)
